scikit-learnで混同行列を生成、適合率・再現率・F1値などを算出
クラス分類問題の結果から混同行列(confusion matrix)を生成したり、真陽性(TP: True Positive)・真陰性(TN: True Negative)・偽陽性(FP: False Positive)・偽陰性(FN: False Negative)のカウントから適合率(precision)・再現率(recall)・F1値(F1-measure)などの評価指標を算出したりすると、そのモデルの良し悪しを判断できる。
scikit-learnのsklearn.metricsモジュールにそれらを簡単に算出するための関数が用意されている。
ここではまず混同行列について説明する。
- 混同行列(confusion matrix)とは
- 混同行列を生成:
confusion_matrix() - TN, FP, FN, TPの個数を取得
- 多クラス分類の混同行列
- ヒートマップで可視化(seaborn使用)
そのあとで評価指標について説明する。
- クラス分類問題における評価指標
- 正解率(accuracy):
accuracy_score() - 適合率(precision):
precision_score() - 再現率(recall):
recall_score() - F1値(F1-measure):
f1_score() - マクロ平均・マイクロ平均・加重平均
- 評価指標をまとめて算出:
classification_report() - 多クラス分類の評価指標
ROC-AUCについてはここでは触れていない。以下の記事を参照。
混同行列(confusion matrix)とは
混同行列(confusion matrix)はクラス分類問題の結果を「実際のクラス」と「予測したクラス」を軸にしてまとめたもの。
二値分類(2クラス分類)においては実際のクラスと予測したクラスの組み合わせによって、結果を以下の4種類に分けることができる。
- 真陽性(TP: True Positive): 実際のクラスが陽性で予測も陽性(正解)
- 真陰性(TN: True Negative): 実際のクラスが陰性で予測も陰性(正解)
- 偽陽性(FP: False Positive): 実際のクラスは陰性で予測が陽性(不正解)
- 偽陰性(FN: False Negative): 実際のクラスは陽性で予測が陰性(不正解)
これを行列にしたものが混同行列。以下のように表される。
Predicted
Negative Positive
Actual Negative TN FP
Positive FN TP
ここで注意すべきは、どの結果を陽性とするかは自分で決める必要があるということ。例えば男女を分類するような問題の場合、男性を陽性としてもいいし女性を陽性としてもいい。後述のようにどちらを陽性とするかによって結果が変わる評価指標もあるので注意。
混同行列を生成: confusion_matrix()
scikit-learnで混同行列を生成するにはconfusion_matrix()を用いる。
第一引数に実際のクラス(正解クラス)、第二引数に予測したクラスのリストや配列を指定する。
NumPy配列ndarrayが返される。
from sklearn.metrics import confusion_matrix
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
cm = confusion_matrix(y_true, y_pred)
print(cm)
# [[1 4]
# [3 2]]
print(type(cm))
# <class 'numpy.ndarray'>
confusion_matrix()自体は正解と予測の組み合わせでカウントした値を行列にしただけで、行列のどの要素が真陽性(TP)かはどのクラスを陽性・陰性と考えるかによって異なる。
各軸は各クラスの値を昇順にソートした順番になる。上の例のように0 or 1の二値分類であれば0, 1の順番。ここで0を陰性(Negative)、1を陽性(Positive)とすると以下のような対応関係になる。
0 = Negative, 1 = Positive
Predicted
0 1
Actual 0 TN FP
1 FN TP
TN, FP, FN, TPの個数を取得
TN, FP, FN, TPの個数を取得したい場合はconfusion_matrix()で得られたndarrayをflatten()メソッドで一次元化して、アンパックで取り出せばよい。
print(cm.flatten())
# [1 4 3 2]
tn, fp, fn, tp = cm.flatten()
print(tn)
# 1
print(fp)
# 4
print(fn)
# 3
print(tp)
# 2
この例は0 or 1の二値分類で、0を陰性(Negative)としているので上のような並びになっている。多くの場合はこれで問題ないが、常にこの並びであるとは限らない。
例えばA or Bの二値分類。
Aを陰性、Bを陽性とすると以下の通り。
A = Negative, B = Positive
Predicted
A B
Actual A TN FP
B FN TP
Aを陽性、Bを陰性とすると以下のようになる。
A = Positive, B = Negative
Predicted
A B
Actual A TP FN
B FP TN
後者の場合、flatten()で一次元化した場合の並びは上の例とは異なりTP, FN, FP, TNとなる。
混同行列のどの要素がTNかなどを毎回考えるのは間違いの元なので、軸の順番を合わせるのがオススメ。confusion_matrix()は引数labelsで軸の順番を指定できる。
y_true_ab = ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B']
y_pred_ab = ['A', 'B', 'B', 'B', 'B', 'A', 'A', 'A', 'B', 'B']
print(confusion_matrix(y_true_ab, y_pred_ab))
# [[1 4]
# [3 2]]
print(confusion_matrix(y_true_ab, y_pred_ab, labels=['B', 'A']))
# [[2 3]
# [4 1]]
0が陰性、1が陽性という順番に合わせて、例えばA, BでもBが陰性であれば上の例の後者のように引数labelsを指定すると以下のような対応関係になる。
A = Positive, B = Negative
Predicted
B A
Actual B TN FP
A FN TP
多クラス分類の混同行列
3クラス以上の多クラス分類でも同様に混同行列を生成できる。
y_true_multi = [0, 0, 0, 1, 1, 1, 2, 2, 2]
y_pred_multi = [0, 1, 1, 1, 1, 2, 2, 2, 2]
print(confusion_matrix(y_true_multi, y_pred_multi))
# [[1 2 0]
# [0 2 1]
# [0 0 3]]
引数labelsを使うと、二値分類の場合と同様に軸の順番を変えられる。さらに、特定のラベルのみの結果を生成することも可能。
print(confusion_matrix(y_true_multi, y_pred_multi, labels=[2, 1]))
# [[3 0]
# [1 2]]
ヒートマップで可視化(seaborn使用)
混同行列を可視化したい場合はseabornのheatmap()関数を使うのが簡単。
from sklearn.metrics import confusion_matrix
import seaborn as sns
import matplotlib.pyplot as plt
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
cm = confusion_matrix(y_true, y_pred)
print(cm)
# [[1 4]
# [3 2]]
sns.heatmap(cm)
plt.savefig('data/dst/sklearn_confusion_matrix.png')
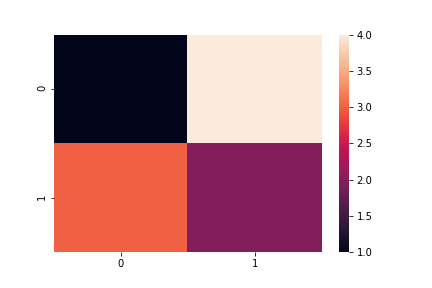
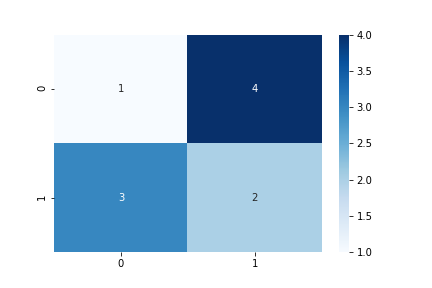
値を表示したり色を変えたりもできる。
sns.heatmap(cm, annot=True, cmap='Blues')
plt.savefig('data/dst/sklearn_confusion_matrix_annot_blues.png')
seabornのheatmap()関数についての詳細は以下の記事を参照。
クラス分類問題における評価指標
上述の真陽性(TP: True Positive)・真陰性(TN: True Negative)・偽陽性(FP: False Positive)・偽陰性(FN: False Negative)の値を利用してクラス分類問題を解くモデルの評価指標を算出できる。
ここでは以下の4つについて説明する。
- 正解率(accuracy)
- 適合率(precision, PPV)
- 再現率(recall, sensitivity, hit rate, TPR)
- F値(F-measure, F-score, F1-score )
上述の通り、混同行列からTP, TN, FP, FNの値を取得してスコアを計算することもできるが、scikit-learnのsklearn.metricsモジュールには実際のクラス(正解クラス)、予測したクラスのリストや配列から直接スコアを算出する関数が用意されている。これらをまとめて算出する便利な関数もある。
なお、TP, TN, FP, FNを利用した評価指標はその他にもたくさんある。Wikipedia(英語版)などを参照。
ROC-AUCについては以下の記事を参照。
正解率(accuracy): accuracy_score()
正解率(accuracy)は、すべてのサンプルのうち正解したサンプルの割合。
$$ \text{accuracy} = \frac{TP + TN}{TP + TN + FP + FN} $$
関数accuracy_score()で算出できる。
from sklearn.metrics import accuracy_score
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(accuracy_score(y_true, y_pred))
# 0.3
適合率(precision): precision_score()
適合率(precision)は、陽性と予測されたサンプルのうち正解したサンプルの割合。PPV(positive predictive value)とも呼ばれる。
$$ \text{precision} = \frac{TP}{TP + FP} $$
FP(偽陽性)が大きくなると適合率は小さくなる。偽陽性を避けたい(抑えたい)場合に指標として用いる。
関数precision_score()で算出できる。
from sklearn.metrics import precision_score
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(precision_score(y_true, y_pred))
# 0.3333333333333333
適合率はどのクラスを陽性とするか(陰性とするか)によって値が異なる。これについての詳細は後述。
再現率(recall): recall_score()
再現率(recall)は実際に陽性のサンプルのうち正解したサンプルの割合。sensitivityやhit rate, TPR(true positive rate, 真陽性率)などとも呼ばれる。
$$ \text{recall} = \frac{TP}{TP + FN} $$
FN(偽陰性)が大きくなると再現率は小さくなる。偽陰性を避けたい(抑えたい)場合に指標として用いる。
関数recall_score()で算出できる。
from sklearn.metrics import recall_score
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(recall_score(y_true, y_pred))
# 0.4
再現率も適合率と同様にどのクラスを陽性とするか(陰性とするか)によって値が異なる。これについての詳細は後述。
F1値(F1-measure): f1_score()
F1値(F1-measure)は適合率と再現率の調和平均。 単純にF値(F-measure, F-score)と呼ばれることもある。
$$ \text{F1-measure} = \frac{2 * \text{precision} * \text{recall}}{\text{precision} + \text{recall}} = \frac{2 * TP}{2 * TP + FP + FN} $$
関数f1_score()で算出できる。
from sklearn.metrics import f1_score
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(f1_score(y_true, y_pred))
# 0.3636363636363636
なお、F1値はより一般的な表現である$F_\beta$値のβ=1とした場合の値。詳細は以下の記事を参照。
F1値も適合率、再現率と同様にどのクラスを陽性とするか(陰性とするか)によって値が異なる。これについての詳細は後述。
マクロ平均・マイクロ平均・加重平均
適合率、再現率、F1値はどのクラスを陽性とするか(陰性とするか)によって値が異なる。
ここでは適合率を例として説明する。再現率、F1値でも考え方は同じ。
precision_score()などの関数は、デフォルトでは1を陽性(Positive)として値を算出する。
from sklearn.metrics import precision_score
from sklearn.metrics import confusion_matrix
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(precision_score(y_true, y_pred))
# 0.3333333333333333
引数pos_labelで陽性とするクラスを指定できる。pos_label=0とすると、0が陽性、1が陰性として値が算出される。
print(precision_score(y_true, y_pred, pos_label=0))
# 0.25
引数averageを指定することで、陽性・陰性を入れ替えた結果を考慮した値が算出される。
average=Noneとすると、0, 1をそれぞれ陽性としたときの値がリストで返される。
print(precision_score(y_true, y_pred, average=None))
# [0.25 0.33333333]
average='macro'はマクロ平均。陽性・陰性を入れ替えて算出した2つの値の算術平均となる。
print(precision_score(y_true, y_pred, average='macro'))
# 0.29166666666666663
average='micro'はマイクロ平均。陽性・陰性を入れ替えたそれぞれの状態でのTPやFP, FNの合計から適合率などを算出する。
print(precision_score(y_true, y_pred, average='micro'))
# 0.3
各状態の混合行列とTP, FPなどの対応は以下の通り。
print(confusion_matrix(y_true, y_pred))
# [[1 4]
# [3 2]]
print(confusion_matrix(y_true, y_pred, labels=[1, 0]))
# [[2 3]
# [4 1]]
0 = Negative, 1 = Positive
Predict
0 1
Actual 0 TN FP
1 FN TP
0 = Positive, 1 = Negative
Predict
1 0
Actual 1 TN FP
0 FN TP
各状態での値を合計すると、
precision = TP / (TP + FP) = (2 + 1) / ((2 + 1) + (4 + 3)) = 0.3
となっていることが分かる。
average='weighted'は陽性・陰性を変えて算出した2つの値の加重平均。正解のクラスの個数に応じて加重平均する。
この例は0も1も同数(5個ずつ)なのでaverage='macro'の算術平均と同じ。差がある例は次に示す。
print(precision_score(y_true, y_pred, average='weighted'))
# 0.29166666666666663
ここまでの例では引数averageを変えても結果はあまり変わらないが、正解のクラスの個数に偏りがあったり、陽性・陰性を変えた場合の値の差が大きかったりするとaverageの指定によって結果が大きく変わる。
y_true_2 = [0, 1, 1, 1, 1]
y_pred_2 = [0, 0, 0, 0, 1]
print(confusion_matrix(y_true_2, y_pred_2))
# [[1 0]
# [3 1]]
print(confusion_matrix(y_true_2, y_pred_2, labels=[1, 0]))
# [[1 3]
# [0 1]]
print(precision_score(y_true_2, y_pred_2))
# 1.0
print(precision_score(y_true_2, y_pred_2, pos_label=0))
# 0.25
print(precision_score(y_true_2, y_pred_2, average='macro'))
# 0.625
print(precision_score(y_true_2, y_pred_2, average='micro'))
# 0.4
print(precision_score(y_true_2, y_pred_2, average='weighted'))
# 0.85
ここではaverage='weighted'は
(pos_label=0の結果 * 0の個数 + pos_label=1の結果 * 1の個数) / 全個数
= (0.25 * 1 + 1.0 * 4) / 5 = 0.85
となる。
マクロ平均・マイクロ平均・加重平均のいずれを使うかは状況によって異なる。
例えば2つ目の例のように正解のクラスの個数に偏りがあると、単純な算術平均であるマクロ平均では個数が少ないクラスの結果の影響がマイクロ平均よりも相対的に大きくなる。個数が少ないクラスの重要度が低い場合はマイクロ平均のほうが適しているだろうし、個数によらずすべてのクラスの結果を反映させたい場合はマクロ平均のほうが適しているだろう。
付随する注意点として、pos_label=1がデフォルトなので1が含まれていないリストや配列はエラーとなる。そのような場合はpos_labelを明示的に指定する必要がある。
y_true_ab = ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B']
y_pred_ab = ['A', 'B', 'B', 'B', 'B', 'A', 'A', 'A', 'B', 'B']
# print(precision_score(y_true_ab, y_pred_ab))
# ValueError: pos_label=1 is not a valid label: array(['A', 'B'], dtype='<U1')
print(precision_score(y_true_ab, y_pred_ab, pos_label='A'))
# 0.25
評価指標をまとめて算出: classification_report()
適合率、再現率、F1値およびそれらのマクロ平均、マイクロ平均、加重平均を算出してくれるclassification_report()関数がある。便利。
マクロ平均、マイクロ平均、加重平均を出力するようになったのはバージョン0.20から。
文字列で結果が返される。なお、supportはy_trueにおける各クラスの個数。
from sklearn.metrics import classification_report
import pandas as pd
import pprint
y_true = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
y_pred = [0, 1, 1, 1, 1, 0, 0, 0, 1, 1]
print(classification_report(y_true, y_pred))
# precision recall f1-score support
#
# 0 0.25 0.20 0.22 5
# 1 0.33 0.40 0.36 5
#
# micro avg 0.30 0.30 0.30 10
# macro avg 0.29 0.30 0.29 10
# weighted avg 0.29 0.30 0.29 10
#
print(type(classification_report(y_true, y_pred)))
# <class 'str'>
1行目、2行目(0, 1)はそれぞれの値をpos_labelとしたときの結果。引数target_namesで任意の名前に変更することも可能。
print(classification_report(y_true, y_pred,
target_names=['class_0', 'class_1']))
# precision recall f1-score support
#
# class_0 0.25 0.20 0.22 5
# class_1 0.33 0.40 0.36 5
#
# micro avg 0.30 0.30 0.30 10
# macro avg 0.29 0.30 0.29 10
# weighted avg 0.29 0.30 0.29 10
#
バージョン0.20から引数output_dictが追加され、これをTrueとすると文字列ではなく辞書を返すようになった。ここではpprintを使って見やすく表示している。
d = classification_report(y_true, y_pred, output_dict=True)
pprint.pprint(d)
# {'0': {'f1-score': 0.22222222222222224,
# 'precision': 0.25,
# 'recall': 0.2,
# 'support': 5},
# '1': {'f1-score': 0.3636363636363636,
# 'precision': 0.3333333333333333,
# 'recall': 0.4,
# 'support': 5},
# 'macro avg': {'f1-score': 0.29292929292929293,
# 'precision': 0.29166666666666663,
# 'recall': 0.30000000000000004,
# 'support': 10},
# 'micro avg': {'f1-score': 0.3, 'precision': 0.3, 'recall': 0.3, 'support': 10},
# 'weighted avg': {'f1-score': 0.29292929292929293,
# 'precision': 0.29166666666666663,
# 'recall': 0.3,
# 'support': 10}}
各指標の値を数値で取得できる。
print(d['0'])
# {'precision': 0.25, 'recall': 0.2, 'f1-score': 0.22222222222222224, 'support': 5}
print(d['0']['precision'])
# 0.25
print(type(d['0']['precision']))
# <class 'float'>
さらにこの辞書からpandas.DataFrameを生成することも可能。
df = pd.DataFrame(d)
print(df)
# 0 1 micro avg macro avg weighted avg
# f1-score 0.222222 0.363636 0.3 0.292929 0.292929
# precision 0.250000 0.333333 0.3 0.291667 0.291667
# recall 0.200000 0.400000 0.3 0.300000 0.300000
# support 5.000000 5.000000 10.0 10.000000 10.000000
print(df.iloc[:, :-3])
# 0 1
# f1-score 0.222222 0.363636
# precision 0.250000 0.333333
# recall 0.200000 0.400000
# support 5.000000 5.000000
print(df.iloc[:, -3:])
# micro avg macro avg weighted avg
# f1-score 0.3 0.292929 0.292929
# precision 0.3 0.291667 0.291667
# recall 0.3 0.300000 0.300000
# support 10.0 10.000000 10.000000
上の例のように所望の結果のみを選択したりするのが簡単。CSVなど様々なフォーマットに出力するのにも便利。
多クラス分類の評価指標
ここまでの評価指標の例はすべて二値分類(2クラス分類)だったが、最後に多クラス分類の場合について説明する。
以下の3クラス分類を例とする。
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
from sklearn.metrics import classification_report
y_true_multi = [0, 0, 0, 1, 1, 1, 2, 2, 2]
y_pred_multi = [0, 1, 1, 1, 1, 2, 2, 2, 2]
print(confusion_matrix(y_true_multi, y_pred_multi))
# [[1 2 0]
# [0 2 1]
# [0 0 3]]
precision_score()などの関数はデフォルトで二値分類を想定しているので、多クラスの配列をy_true, y_predに指定するとエラーになる。
引数averageを指定すると値が算出される。
# print(precision_score(y_true_multi, y_pred_multi))
# ValueError: Target is multiclass but average='binary'. Please choose another average setting.
print(precision_score(y_true_multi, y_pred_multi, average=None))
# [1. 0.5 0.75]
print(precision_score(y_true_multi, y_pred_multi, average='macro'))
# 0.75
print(precision_score(y_true_multi, y_pred_multi, average='micro'))
# 0.6666666666666666
print(precision_score(y_true_multi, y_pred_multi, average='weighted'))
# 0.75
多クラス分類においてある一つのクラスに注目したとき、そのクラスを陽性、そのほかのすべてのクラスを陰性とする二値分類と考えることができる。
例えば、0を陽性、1, 2を陰性とする二値分類と考えた場合、混同行列におけるTPなどの対応は以下のようになる。
0 = Positive, 1 = 2 = Negative
predicted
0 1 2
Actual 0 TP FN FN
1 FP TN TN
2 FP TN TN
実際に計算してみると分かるように、average=Noneとしたときに返される各クラスの値はこの考え方をもとに算出されている。
各クラスの値の平均であるマクロ平均、マイクロ平均、加重平均の算出方法は二値分類の場合と同じ。
recall_score()、f1_score()もprecision_score()と同様に引数averageを指定する必要がある。
classification_report()では各クラスをそれぞれ陽性としたときの値とそれらの平均がまとめて算出される。
print(classification_report(y_true_multi, y_pred_multi))
# precision recall f1-score support
#
# 0 1.00 0.33 0.50 3
# 1 0.50 0.67 0.57 3
# 2 0.75 1.00 0.86 3
#
# micro avg 0.67 0.67 0.67 9
# macro avg 0.75 0.67 0.64 9
# weighted avg 0.75 0.67 0.64 9
#