scikit-learnでROC曲線とそのAUCを算出
機械学習の分類問題などの評価指標としてROC-AUCが使われることがある。ROCはReceiver operating characteristic(受信者操作特性)、AUCはArea under the curveの略で、Area under an ROC curve(ROC曲線下の面積)をROC-AUCなどと呼ぶ。
scikit-learnを使うと、ROC曲線を算出・プロットしたり、ROC-AUCスコアを算出できる。
- sklearn.metrics.roc_curve — scikit-learn 0.20.3 documentation
- sklearn.metrics.roc_auc_score — scikit-learn 0.20.3 documentation
ここでは以下の内容について説明する。
- ROC曲線を算出・プロット:
roc_curve() - ROC曲線の意味
- FPR(偽陽性率)とTPR(真陽性率)
- 様々なROC曲線
- ROC曲線の特徴と注意点
- ROC曲線に影響するのは予測スコアの順番(順位)のみ
- ランダムに分類した場合のROC曲線
- AUCの意味
- ROC-AUCスコアの算出:
roc_auc_score()
混同行列や適合率・再現率など、より基本的な評価指標については以下の記事を参照。
ROC曲線を算出・プロット: roc_curve()
ROC曲線の算出にはsklearn.metricsモジュールのroc_curve()関数を使う。
第一引数に正解クラス、第二引数に予測スコアのリストや配列をそれぞれ指定する。
予測スコアは機械学習のモデルなどによって予測された確率で、例えば1.0だと100%の確率で1だと予測、0.8だと80%の確率で1だと予測しているという意味合いの値。
roc_curve()は3つの要素を持つタプルを返す。
from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt
y_true = [0, 0, 0, 0, 1, 1, 1, 1]
y_score = [0.2, 0.3, 0.6, 0.8, 0.4, 0.5, 0.7, 0.9]
roc = roc_curve(y_true, y_score)
print(type(roc))
# <class 'tuple'>
print(len(roc))
# 3
3つの要素は順番にfpr, tpr, thresholdsで、それぞれFPR(偽陽性率)、TPR(真陽性率)、閾値。詳細は後述。
ここではアンパックでそれぞれの変数に格納して中身を確認する。
fpr, tpr, thresholds = roc_curve(y_true, y_score)
print(fpr)
# [0. 0. 0.25 0.25 0.5 0.5 1. ]
print(tpr)
# [0. 0.25 0.25 0.5 0.5 1. 1. ]
print(thresholds)
# [1.9 0.9 0.8 0.7 0.6 0.4 0.2]
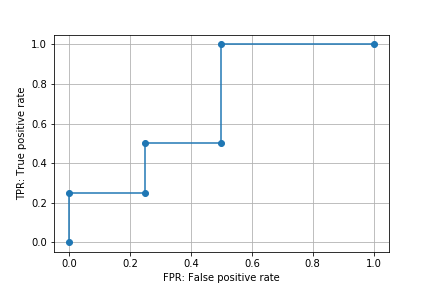
このfprを横軸、tprを縦軸にプロットしたものをROC曲線と呼ぶ。
plt.plot(fpr, tpr, marker='o')
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve.png')
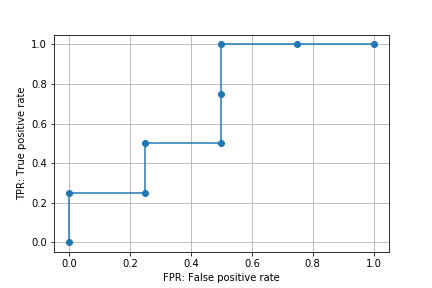
roc_curve()関数はデフォルトでROC曲線の形状に影響しない点を省略(除外)するようになっている。引数drop_intermediateをFalseとするとすべての点が省略されずに算出される。
fpr_all, tpr_all, thresholds_all = roc_curve(y_true, y_score,
drop_intermediate=False)
print(fpr_all)
# [0. 0. 0.25 0.25 0.5 0.5 0.5 0.75 1. ]
print(tpr_all)
# [0. 0.25 0.25 0.5 0.5 0.75 1. 1. 1. ]
print(thresholds_all)
# [1.9 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2]
plt.plot(fpr_all, tpr_all, marker='o')
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve_all.png')
また、陽性クラスを指定するための引数pos_labelもある。0 or 1の二値分類の場合は気にする必要はないが、そのほかのクラス(ラベル)を使う場合はpos_labelで明示的に指定する必要がある。
ROC曲線の意味
正解クラスと予測スコアが与えられたとき、各予測スコアを閾値としたときのFPR(偽陽性率)を横軸、TPR(真陽性率)を縦軸にプロットしたものがROC曲線。
これだけだと意味が分からないので順を追って見ていく。
上の例と同じ正解クラス、予測スコアをNumPy配列ndarrayとして定義する。
from sklearn.metrics import roc_curve, recall_score, confusion_matrix
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
y_true = np.array([0, 0, 0, 0, 1, 1, 1, 1])
y_score = np.array([0.2, 0.3, 0.6, 0.8, 0.4, 0.5, 0.7, 0.9])
FPR(偽陽性率)とTPR(真陽性率)
予測スコアはあくまでも確率なので、0 or 1を判定し分類するには閾値を指定する必要がある。
例えば0.5を閾値としてそれ以上を1と判定すると結果は以下のようになる。
ndarrayを比較演算子で比較するとboolのndarrayが得られるのでそれをastype()で整数intに変換している。なお、intに変換しているのは表示上見やすくするためで、計算する上ではboolのままで問題ない(Falseが0、Trueが1とみなされる)。
print(y_score >= 0.5)
# [False False True True False True True True]
print((y_score >= 0.5).astype(int))
# [0 0 1 1 0 1 1 1]
0 or 1の判定結果が得られると、それを正解クラスと比較することでFPRやTPRを算出できる。FPR, TPRの定義は以下の通り。
-
FPR: false positive rate(偽陽性率)
- 陰性を間違って陽性と判定した割合
- 小さい方が良い
FPR = FP / (FP + TN)
- 陰性を間違って陽性と判定した割合
-
TPR: true positive rate(真陽性率)
- 陽性を正しく陽性と判定した割合
- 大きいほうが良い
- recall(再現率)やsensitivity, hit rateなどとも呼ばれる
TPR = TP / (TP + FN)
- 陽性を正しく陽性と判定した割合
ここで、TP, TN, FP, FNの意味は以下の通り。それぞれの個数からFPR, TPRを算出する。
- 真陽性(TP: True Positive): 実際のクラスが陽性で予測も陽性(正解)
- 真陰性(TN: True Negative): 実際のクラスが陰性で予測も陰性(正解)
- 偽陽性(FP: False Positive): 実際のクラスは陰性で予測が陽性(不正解)
- 偽陰性(FN: False Negative): 実際のクラスは陽性で予測が陰性(不正解)
このあたりの詳細は以下の記事を参照。
FPRを算出する関数を定義すると、0.5を閾値とした場合のFPRは以下のようになる。なお、この関数は簡易的なもので、0 or 1の二値分類で0を陰性、1を陽性とする場合にのみ対応している。
def fpr_score(y_true, y_pred):
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).flatten()
return fp / (tn + fp)
print(fpr_score(y_true, y_score >= 0.5))
# 0.5
TPRはscikit-learnのrecall_score()関数がそのまま使える。結果は以下の通り。
print(recall_score(y_true, y_score >= 0.5))
# 0.75
FPR, TPRのイメージを掴むために、閾値を極端に振った場合を考える。
閾値を予測スコアの最小値とすると、すべての予測スコアが1(陽性)と判定される。この場合、陽性も陰性もすべて陽性と判定している状態なので、FPRもTPRも1となる。
th_min = min(y_score)
print(th_min)
# 0.2
print((y_score >= th_min).astype(int))
# [1 1 1 1 1 1 1 1]
print(fpr_score(y_true, y_score >= th_min))
# 1.0
print(recall_score(y_true, y_score >= th_min))
# 1.0
閾値を予測スコアの最大値に1を加えた値とすると、すべての予測スコアが0(陰性)と判定される。ここで1を加えているのは最大値をそのまま使うと最大値の予測スコア自身は1(陽性)と判定されてしまうため。最大値よりさらに大きい値になれば加える値はなんでもよい。
この場合、陽性も陰性もすべて陰性と判定している状態なので、FPRもTPRも0となる。
th_max = max(y_score) + 1
print(th_max)
# 1.9
print((y_score >= th_max).astype(int))
# [0 0 0 0 0 0 0 0]
print(fpr_score(y_true, y_score >= th_max))
# 0.0
print(recall_score(y_true, y_score >= th_max))
# 0.0
すべての予測スコアを閾値とした場合のFPRとTPRを算出してみる。pandasのapply()メソッドを使っている。
df = pd.DataFrame({'true': y_true, 'score': y_score})
df['TPR'] = df.apply(lambda row: recall_score(y_true, y_score >= row['score']), axis=1)
df['FPR'] = df.apply(lambda row: fpr_score(y_true, y_score >= row['score']), axis=1)
print(df)
# true score TPR FPR
# 0 0 0.2 1.00 1.00
# 1 0 0.3 1.00 0.75
# 2 0 0.6 0.50 0.50
# 3 0 0.8 0.25 0.25
# 4 1 0.4 1.00 0.50
# 5 1 0.5 0.75 0.50
# 6 1 0.7 0.50 0.25
# 7 1 0.9 0.25 0.00
予測スコアで降順にソートすると以下の通り。
print(df.sort_values('score', ascending=False))
# true score TPR FPR
# 7 1 0.9 0.25 0.00
# 3 0 0.8 0.25 0.25
# 6 1 0.7 0.50 0.25
# 2 0 0.6 0.50 0.50
# 5 1 0.5 0.75 0.50
# 4 1 0.4 1.00 0.50
# 1 0 0.3 1.00 0.75
# 0 0 0.2 1.00 1.00
ここで、roc_curve()関数が返すfpr, tpr, thresholdsを確認する。drop_intermediate=Falseとして省略なしにしている。
fpr_all, tpr_all, th_all = roc_curve(y_true, y_score,
drop_intermediate=False)
df_roc = pd.DataFrame({'th_all': th_all, 'tpr_all': tpr_all, 'fpr_all': fpr_all})
print(df_roc)
# th_all tpr_all fpr_all
# 0 1.9 0.00 0.00
# 1 0.9 0.25 0.00
# 2 0.8 0.25 0.25
# 3 0.7 0.50 0.25
# 4 0.6 0.50 0.50
# 5 0.5 0.75 0.50
# 6 0.4 1.00 0.50
# 7 0.3 1.00 0.75
# 8 0.2 1.00 1.00
2行目以降は上で算出したものと一致していることが確認できる。1行目は予測スコアの最大値に1を加えたものを閾値としてそのFPR, TPRを算出している。最大値に1を加えるのは、すべての予測スコアを0(陰性)と判定してFPRもTPRも0となるポイントを追加するため。
上でも示したようにこのfprを横軸、tprを縦軸にプロットしたものがROC曲線。

様々なROC曲線
ROC曲線が何を意味しているのか、ROC曲線から何が分かるのかを考える。
理想的な例として、適切な閾値を設定すると0(陰性)と1(陽性)を完全に分類できる場合を考える。
y_true_perfect = np.array([0, 0, 0, 0, 1, 1, 1, 1])
y_score_perfect = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8])
この例では閾値を0.5とすると完全に正しく分類できる。0.45でもいいが、ここでは予測スコアに存在する値を使う。
print(y_true_perfect)
# [0 0 0 0 1 1 1 1]
print((y_score_perfect >= 0.5).astype(int))
# [0 0 0 0 1 1 1 1]
この理想的な状態では、FPRは0、TPRは1となる。
print(fpr_score(y_true_perfect, y_score_perfect >= 0.5))
# 0.0
print(recall_score(y_true_perfect, y_score_perfect >= 0.5))
# 1.0
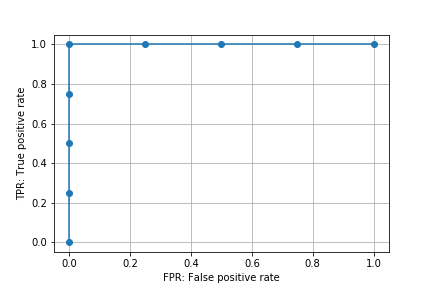
ROC曲線をプロットすると以下のようになる。
roc_p = roc_curve(y_true_perfect, y_score_perfect, drop_intermediate=False)
plt.plot(roc_p[0], roc_p[1], marker='o')
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve_perfect.png')
理想的な例から正解ラベルを変更して、完全に正しく分類できる閾値が存在しない場合のROC曲線を追加する。
y_true_1 = np.array([0, 0, 0, 1, 0, 1, 1, 1])
y_score_1 = y_score_perfect
roc_1 = roc_curve(y_true_1, y_score_1, drop_intermediate=False)
y_true_2 = np.array([0, 0, 1, 1, 0, 0, 1, 1])
y_score_2 = y_score_perfect
roc_2 = roc_curve(y_true_2, y_score_2, drop_intermediate=False)
plt.plot(roc_p[0], roc_p[1], marker='s')
plt.plot(roc_1[0], roc_1[1], marker='o')
plt.plot(roc_2[0], roc_2[1], marker='x')
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve_compare.png')
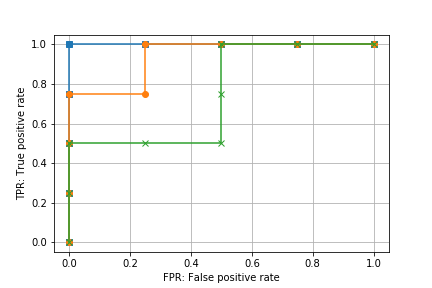
このグラフから、ROC曲線は、
- 理想的な予測(分類)ができていると
(FPR, TPR) = (0, 1)(左上の点)を通る - 理想的な予測からずれると
(FPR, TPR) = (0, 1)(左上の点)から離れていく
ことが分かる。ROC曲線が左上に膨らむほど正しく予測ができているというイメージ。
正しく予測できていると閾値を大きくしていったときにFPRが小さいままTPRが大きくなっていき、正しく予測できていないと閾値を大きくしていったときにTPRが小さいままFPRが大きくなっていく。ROC曲線はそのようなFPRとTPRの関係を図示したものと考えることもできる。
これを数値化するために、ROC曲線のAUC(曲線下の面積)を算出する方法がある。これについては後述。
ROC曲線の特徴と注意点
ROC曲線に影響するのは予測スコアの順番(順位)のみ
予測スコアを閾値にしてFPRとTPRを算出していくという性質上、ROC曲線に影響を与えるのは予測スコアの順番(順位)のみ。
順位が変わらなければ、スコアの絶対値が変わったりスコア間の間隔が変わっても同じ曲線となる。
y_true_org = np.array([0, 0, 1, 1, 0, 0, 1, 1])
y_score_org = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8])
roc_org = roc_curve(y_true_org, y_score_org, drop_intermediate=False)
y_score_scale = y_score_org / 2
print(y_score_scale)
# [0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 ]
roc_scale = roc_curve(y_true_org, y_score_scale, drop_intermediate=False)
y_score_interval = np.array([0.01, 0.02, 0.91, 0.92, 0.93, 0.94, 0.95, 0.96])
roc_interval = roc_curve(y_true_org, y_score_interval, drop_intermediate=False)
plt.plot(roc_org[0], roc_org[1], marker='s')
plt.plot(roc_scale[0], roc_scale[1], marker='o', linestyle='-.')
plt.plot(roc_interval[0], roc_interval[1], marker='x', linestyle=':')
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve_same.png')
分かりにくいかもしれないが、すべてのグラフが重なっている。

ROC曲線が同じだと次に説明するROC-AUCスコアの値も同じ。共通の正解ラベルに対して、様々なモデルで算出した予測スコアが異なる値でも、その順位が同じだとROC曲線およびROC-AUCスコアの値も同じになる。
リストや配列の順位を取得するにはpandasのrank()が便利。
s = pd.Series(y_score_interval)
print(s)
# 0 0.01
# 1 0.02
# 2 0.91
# 3 0.92
# 4 0.93
# 5 0.94
# 6 0.95
# 7 0.96
# dtype: float64
print(s.rank())
# 0 1.0
# 1 2.0
# 2 3.0
# 3 4.0
# 4 5.0
# 5 6.0
# 6 7.0
# 7 8.0
# dtype: float64
ランダムに分類した場合のROC曲線
ランダムに分類した場合、サンプル数が多ければROC曲線は(0, 0)(左下の点)と(1, 1)(右上の点)を結ぶ線となる。
np.random.seed(0)
y_true_random = np.array([0] * 5000 + [1] * 5000)
y_score_random = np.random.rand(10000)
roc_random = roc_curve(y_true_random, y_score_random)
plt.plot(roc_random[0], roc_random[1])
plt.xlabel('FPR: False positive rate')
plt.ylabel('TPR: True positive rate')
plt.grid()
plt.savefig('data/dst/sklearn_roc_curve_random.png')
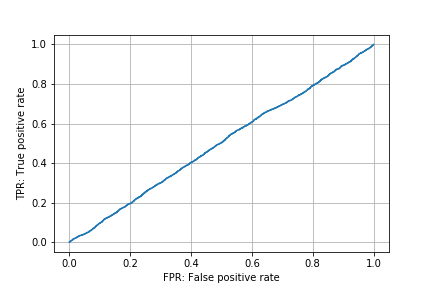
分類の性能が悪いと、ROC曲線はこの直線に近づいていく。
AUCの意味
AUCはArea under the curveの略。曲線下の面積を意味する。
scikit-learnには任意の曲線のAUCを算出する関数auc()がある。
曲線のx座標、y座標をそれぞれ引数に指定するとその曲線下の面積(AUC)が算出される。例えば、roc_curve()で取得できるfpr, tprをauc()の引数に指定するとROC曲線のAUCが算出できる。
ただし、ROC-AUCの場合、直接その値を算出する関数roc_auc_score()があるのでそちらを使ったほうが便利。次に説明する。
ROC-AUCスコアの算出: roc_auc_score()
ROC-AUCスコアの算出にはsklearn.metricsモジュールのroc_auc_score()関数を使う。
roc_curve()関数と同様、第一引数に正解クラス、第二引数に予測スコアのリストや配列をそれぞれ指定する。
上で作成したROC曲線のグラフと合わせて結果を示す。

from sklearn.metrics import roc_auc_score
import numpy as np
y_true = np.array([0, 0, 0, 0, 1, 1, 1, 1])
y_score = np.array([0.2, 0.3, 0.6, 0.8, 0.4, 0.5, 0.7, 0.9])
print(roc_auc_score(y_true, y_score))
# 0.6875
完全に正確に分類できる閾値が存在する場合。

y_true_perfect = np.array([0, 0, 0, 0, 1, 1, 1, 1])
y_score_perfect = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8])
print(roc_auc_score(y_true_perfect, y_score_perfect))
# 1.0
このように、理想的な分類ができるモデルのROC-AUCスコアは1.0となる。
上述のように、ランダムに分類した場合、サンプル数が多ければROC曲線は(0, 0)(左下の点)と(1, 1)(右上の点)を結ぶ線に近づく。このとき、ROC-AUCスコアは0.5に近づく。

np.random.seed(0)
y_true_random = np.array([0] * 5000 + [1] * 5000)
y_score_random = np.random.rand(10000)
print(roc_auc_score(y_true_random, y_score_random))
# 0.49895535999999996
ROC-AUCスコアが0.5を下回る場合は予測スコアを反転すると0.5を上回るようになる。ここで「反転」とは例えば予測スコアが0.0 ~ 1.0の確率の場合、1.0から元の予測スコアを引いた値を新たな予測スコアにする、という意味。
以下は参考のためにROC-AUCスコアが0.5以上の予測スコアを反転した例。ROC-AUCスコアは1 - 元のROC-AUCスコアとなる。
y_score_inv = 1 - y_score
print(y_score_inv)
# [0.8 0.7 0.4 0.2 0.6 0.5 0.3 0.1]
print(roc_auc_score(y_true, y_score_inv))
# 0.3125
y_score_perfect_inv = 1 - y_score_perfect
print(y_score_perfect_inv)
# [0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2]
print(roc_auc_score(y_true_perfect, y_score_perfect_inv))
# 0.0
0.5を下回る場合、分類はできているが予測スコアとクラス(ラベル)の対応が逆になっている。例えば予測スコアが0.8のとき、本来であれば1である確率が80%なのに0である確率が80%になってしまっているというような状態。モデル作成時の単純なミスである可能性が高い。
ROC-AUCスコアを分類モデルの評価指標と考えた場合、その値と分類性能は以下のような関係になる。
0.5が最も悪い(ランダムと同じ = まったく分類できていない)1.0が最も良い(理想的な分類ができる)0.5以上であれば値が大きいほど良い
0.5を下回る場合は予測スコアとクラス(ラベル)の対応が逆になっている- 修正は必要だが分類はできている
0.5以下であれば値が小さいほど分類自体の性能は良い